로또에 당첨될 확률

Table of Contents

• Introduction

• 확률이란?

• 확률의 공리적 정의란?

• 조건부확률이란?

• Reference

 

Introduction

 어떤이는 한주를 로또를 기대하는 마음으로 보내기도 하고 어떤이는 매주마다 추첨하는 로또를 보면서 1등에 당첨됐으면 하는 바람을 가지고 있다. 2002년 12월 7일을 시작으로 매주마다 추첨했던 로또는 오늘날짜 기준으로 로또는 915회차를 진행해왔으며, 약 54조원어치 판매를 달성하였으며, 절반에 해당하는 약 27조가 당첨금으로 사용되었다. 로또는 45개의 숫자 중에서 순서와 관계없이 6개의 숫자가 일치하면 1등에 당첨된다. 이때, 1등에 당첨될 확률은 8,145,060분의 1이란 결과가 나온다.

 

<그림 1> 로또 추첨 기계

 

확률이란?

 로또에 당첨될 확률이 저렇게 낮은데, 도대체 확률이란 무엇인가? 우리는 주사위를 굴렸을 때 나오는 모든 숫자가 무엇인지 이미 잘 알고 있다. 주사위를 굴렸을 때 나타나는 값은 1부터 6까지이며, 이들을 표본공간(Sample Space)라고 부르며 S로 표현한다.

 

S = {1, 2, 3, 4, 5, 6}

 

<그림 2> 주사위

 한 공장에서 생산한 배터리 수명시간을 관측했을 때, 수명시간은 0보다 큰 모든 숫자가 나타날 것이다.

 

S = {t | t ≥ 0}

 

 앞선 두 예시 중에서 주사위와 같이 표본 공간의 원소를 하나씩 셀 수 있는 경우에는, 이산표본공간(Discrete Sample Space)이라고 하고, 배터리 수명시간과 같이 표본 공간의 원소가 셀 수 없는 경우에는 연속표본공간(Continuous Sample Space)이라 한다. 여기서, 주사위를 굴렸을 때 나올 수 있는 모든 원소의 집합인  원소를 사건(Event)라고 부른다.

 

 프랑스의 천문학자이자 수학자인 피에르 시몽 라플라스(1749 ~ 1827)은 어떤 일(사건 = A)이 일어날 수 있는 가능성을 측정하기 위해 확률(Probability)을 정의하였으며, 이를 확률의 고전적 정의라고 부른다.

<그림 3> Pierre Simon de Marquis Laplace

사건 A가 발생할 확률은 N개로 구성된 표본 공간에서 사건 A가 m번 발생하는 것

 

 주사위를 던져서 1이 나올 확률은 6가지의 표본공간(N)에 1이 나올 사건의 수(m)는 1이기에 1/6이며, 주사위를 던졌을 때 짝수가 나올 확률은 6가지의 표본공간(N)에 짝수가 나올 사건의 수(m) = 3이므로 3/6 = 1/2이 된다. 

 

확률의 공리적 정의(Axiomatic definition of Probability)란?

 라플라스는 표본공간에서 발생하는 사건이 유한할 경우에 대한 확률을 정의했다. 하지만, 사건이 발생하는 결과가 무수히 많은 경우가 존재하며, 이를 위한 일반화된 확률의 정의가 필요하다.

 

 통계적 실험을 반복하다보면, 한 사건이 발생하는 것은 일정한 법칙을 따른다는 것을 경험을 통해 알 수 있다. 특히, 한 가지의 사건이 일정한 상수를 향해 간다는 것을 경험적으로 알 수 있다. 이를 우리는 통계적 규칙성이라고 한다.

 

 한 공장에서 생산한 제품을 뽑아 정상인지 불량인지 찾기 위한 실험을 했다. 100개를 뽑았을 때 발생하는 불량 갯수와 200개를 뽑았을 때 발생하는 불량 갯수들을 비율로 나타냈을 경우 일정한 지표에서 왔다갔다 하는 것을 확인 할 수 있다. 이 숫자를 우리는 제품의 불량률이라고 한다.

 

 이를 통해 우리는 통계적 실험을 반복하게 되면 어떤 사건의 수가 근사적으로 사건의 발생할 확률 P(A)에 가까워 진다는 것을 알 수 있다. 이러한 논리는 구소련의 수학자 콜모고로프(1903 ~ 1987)에 의해 확률을 정의한 것이 확률의 공리적 정의이다.

<그림 3> Andrey Nikolaevich Kolmogorov

 - 표본공간(S)에서 발생하는 사건(A)는 0부터 1사이의 값

 - P(S)는 1

 - 서로 배반인 사건의 합은 모든 사건의 합집합을 만족할 때 P(A)를 사건 A의 확률

 

조건부확률(Conditional Probability)이란?

 사건 A가 발생하는 경우는 사건 A의 여사건에서는 결코 발생할 수 없다. 이는 결국 A가 발생할 모든 가능한 집합이 표본공간으로 간주할 수 있으며, 이때 A가 발생하고 B가 일어날 확률은 P(A∩B)/P(A)로 정의한다. 즉, 사건 A가 발생하고 B의 조건부확률을 P(B|A)로 나타낸다.

 

 조건부 확률의 정의에 따라 P(A) > 0, P(B) >0 경우 다음과 같은 승법공식이 성립한다.

 

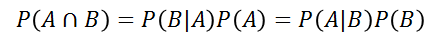
Reference

김우철 외, "현대통계학 4th"

동행복권, "추첨기계 사진", https://www.dhlottery.co.kr/gameInfo.do?method=lotEquip

인명사전, "라플라스", https://terms.naver.com/entry.nhn?docId=879652&cid=43671&categoryId=43671

위키피디아, "콜모고로프", https://en.wikipedia.org/wiki/Andrey_Kolmogorov